连通图：在无向图中，每对顶点之间都有路径可达；

强连通图：在有向图中，每对顶点之间都有路径可达；

连通网：在有向图中，若连接两个顶点之间的边用一个数表示，这个数称为权，权具有特定的意义，代表这条边的代价；

生成树：一个连通图，它包含所有的n个顶点，且这个图中有n-1条边，一个生成树有且仅有n个顶点和n-1条边，若增加一条边，则构成环，若减少一条边，则不是连通图；

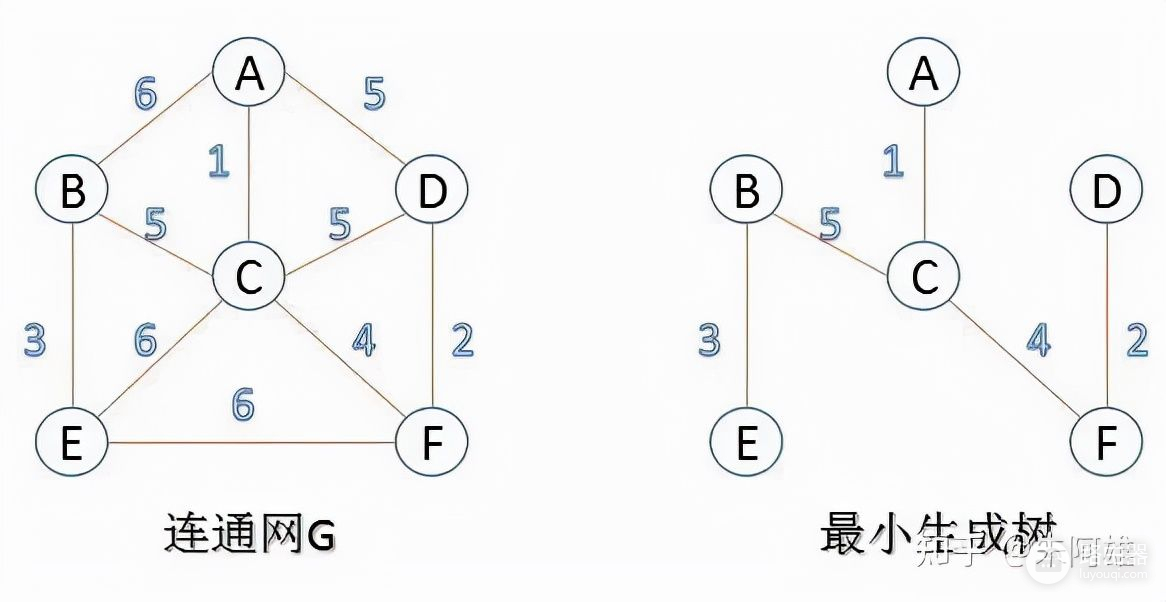
最小生成树：在连通网的所有生成树中，权的和最小的生成树。

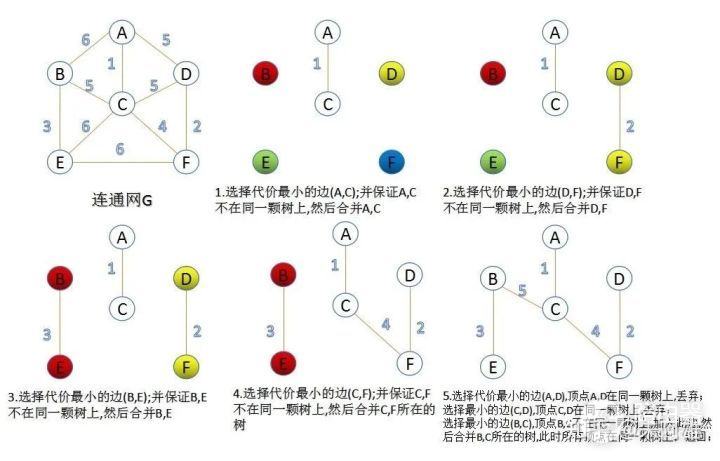
Kruskal算法

初始最小生成树边数为0，每次迭代找权最小的边加入最小生成树边的集合中，但不能形成环；

  1. 将图中边按照权从小到大排序；
  2. 从小到大选择边，且选择的边不构成环，则加入最小生成树边的集合，若构成环，则继续选择下一条稍大且不构成环的边加入集合；
  3. 重复2，直到集合中边的数目为n-1。

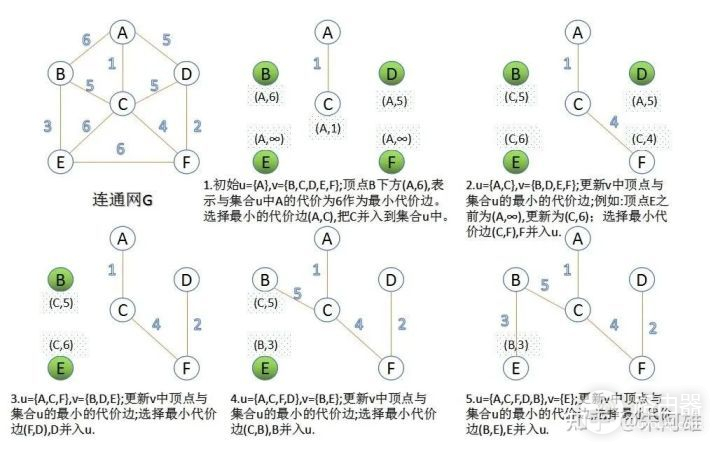
Prim算法

首先从权最小的边开始，选择这条边的一个顶点加入最小生成树顶点集合，一直到所有顶点都加入集合，且不构成环；

  1. 设图中所有顶点集合为V，初始顶点集合u={s}，v=V-u；
  2. 从u和v中找两个顶点u0和v0，两个顶点间边的权最小，将v0加入集合u中；
  3. 重复2，知道集合u的大小为n。

注：凡属于本公众号内容，未经允许不得私自转载，否则将依法追究侵权责任。