余弦距离
余弦距离,也称为余弦相似度,是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。
向量,是多维空间中有方向的线段,如果两个向量的方向一致,即夹角接近零,那么这两个向量就相近。而要确定两个向量方向是否一致,这就要用到余弦定理计算向量的夹角。
余弦定理描述了三角形中任何一个夹角和三个边的关系。给定三角形的三条边,可以使用余弦定理求出三角形各个角的角度。假定三角形的三条边为a,b和c,对应的三个角为A,B和C,那么角A的余弦为:
如果将三角形的两边b和c看成是两个向量,则上述公式等价于:
其中分母表示两个向量b和c的长度,分子表示两个向量的内积。
举一个具体的例子,假如新闻X和新闻Y对应向量分别是:
x1, x2, …, x6400和
y1, y2, …, y6400
则,它们之间的余弦距离可以用它们之间夹角的余弦值来表示:
当两条新闻向量夹角余弦等于1时,这两条新闻完全重复(用这个办法可以删除爬虫所收集网页中的重复网页);当夹角的余弦值接近于1时,两条新闻相似(可以用作文本分类);夹角的余弦越小,两条新闻越不相关。




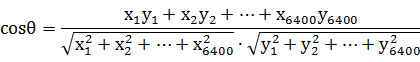

 支付宝扫一扫
支付宝扫一扫 微信扫一扫
微信扫一扫










