BP神经网络是1968年由Rumelhart和Mcclelland为首的科学家提出的概念,是一种按照误差反向传播算法进行训练的多层前馈神经网络,是目前应用比较广泛的一种神经网络结构。BP网络神经网络由输入层、隐藏层和输出层三部分构成,无论隐藏层是一层还是多层,只要是按照误差反向传播算法构建起来的网络(不需要进行预训练,随机初始化后直接进行反向传播),都称为BP神经网络。BP神经网络在单隐层的时候,效率较高,当堆积到多层隐藏层的时候,反向传播的效率就会大大降低,因此BP神经网络在浅层神经网路中应用较广,但由于其隐层数较少,所以映射能力也十分有限,所以浅层结构的BP神经网络多用于解决一些比较简单的映射建模问题。
在深层神经网络中,如果仍采用BP的思想,就得到了BP深层网络结构,即BP-DNN结构。由于隐藏层数较多(通常在两层以上),损失函数关于W,b的偏导自顶而下逐层衰减,等传播到最底层的隐藏层时,损失函数关于W,b的偏导就几乎为零了。如此训练,效率太低,需要进行很长很长时间的训练才行,并且容易产生局部最优问题。因此,便有了一些对BP-DNN进行改进的方法,例如,采用ReLU的激活函数来代替传统的sigmoid函数,可以有效地提高训练的速度。此外,除了随机梯度下降的反向传播算法,还可以采用一些其他的高效的优化算法,例如小批量梯度下降算法(Mini-batch Gradient Descent)、冲量梯度下降算法等,也有利于改善训练的效率问题。直到2006年,Hinton提出了逐层贪婪预训练受限玻尔兹曼机的方法,大大提高了训练的效率,并且很好地改善了局部最优的问题,算是开启了深度神经网络发展的新时代。Hinton将这种基于玻尔兹曼机预训练的结构称为深度置信网络结构(DBN),用深度置信网络构建而成的DNN结构,就是本文要重点介绍的一种标准型的DNN结构,即DBN-DNN。
深度置信神经网络
如图一所示,以3层隐藏层结构的DBN-DNN为例,网络一共由3个受限玻尔兹曼机(RBM,Restricted Boltzmann Machine)单元堆叠而成,其中RBM一共有两层,上层为隐层,下层为显层。堆叠成DNN的时,前一个RBM的输出层(隐层)作为下一个RBM单元的输入层(显层),依次堆叠,便构成了基本的DBN结构,最后再添加一层输出层,就是最终的DBN-DNN结构。
图一 深度置信神经网络(DBN-DNN)结构
受限玻尔兹曼机(RBM)是一种具有随机性的生成神经网络结构,它本质上是一种由具有随机性的一层可见神经元和一层隐藏神经元所构成的无向图模型。它只有在隐藏层和可见层神经元之间有连接,可见层神经元之间以及隐藏层神经元之间都没有连接。并且,隐藏层神经元通常取二进制并服从伯努利分布,可见层神经元可以根据输入的类型取二进制或者实数值。
进一步地,根据可见层(v)和隐藏层(h)的取值不同,可将RBM分成两大类,如果v和h都是二值分布,那么它就是Bernoulli-Bernoulli RBM(贝努力-贝努力RBM);如果v是实数,比如语音特征,h为二进制,那么则为Gaussian-Bernoulli RBM(高斯-贝努力RBM)。因此,图一中的RBM1为高斯-贝努力,RBM2和RBM3都是贝努力-贝努力RBM。
既然提到了受限玻尔兹曼机(RBM),就不得不说一下,基于RBM构建的两种模型:DBN和DBM。如图二所示,DBN模型通过叠加RBM进行逐层预训练时,某层的分布只由上一层决定。例如,DBN的v层依赖于h1的分布,h1只依赖于h2的分布,也就是说,h1的分布不受v的影响,确定了v的分布,h1的分布只由h2来确定。而DBM模型为无向图结构,也就是说,DBM的h1层是由h2层和v层共同决定的,它是双向的。如果从效果来看,DBM结构会比DBN结构具有更好的鲁棒性,但是其求解的复杂度太大,需要将所有的层一起训练,不太利于应用。而DBN结构,如果借用RBM逐层预训练的方法,就方便快捷了很多,便于应用,因此应用的比较广泛。
DBN训练与反向调优
1.进行基于RBM的无监督预训练
利用CD-k算法(Contrastive Divergence,对比散度算法)进行权值初始化如下,Hinton 发现k取为1时,就可以有不错的学习效果。
1)随机初始化权值{W,a,b},其中W为权重向量,a是可见层的偏置向量,b为隐藏层的偏置向量,随机初始化为较小的数值(可为0)
其中,M为显元的个数,N为隐元的个数。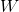
![]() ,其中
,其中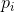
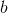
2)将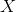
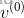
(对于高斯或贝努力可见层神经元)
其中,式中的上标用于区别不同的向量,下标用于区别同一向量中的不同维。
3)根据计算的概率分布进行一步Gibbs抽样,对隐藏层中的每个单元从{0 , 1}中抽取得到相应的值,即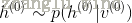
首先,产生一个[0 , 1]上的随机数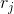
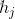
4)用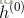
(对于贝叶斯可见层神经元)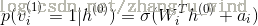
(对于高斯可见层神经元)
其中,N表示为正态分布函数。
5)根据计算到的概率分布,再一次进行一步Gibbs采样,来对显层中的神经元从{0 , 1}中抽取相应的值来进行采样重构,即。详细过程如下:
首先,产生[0 , 1]上的随机数,然后确定的值: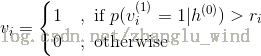
6)再次用显元(重构后的),计算出隐层神经元被开启的概率:
(对于高斯或者贝努力可见层神经元)
7)更新得到新的权重和偏置。
其中,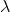
需要说明的是,RBM的训练,实际上是求出一个最能产生训练样本的概率分布。也就是说,要求一个分布,在这个分布里,训练样本的概率最大。由于这个分布的决定性因素在于权值W,所以我们训练的目标就是寻找最佳的权值,以上便是Hinton于2002年提出的名为对比散度学习算法,来寻找最佳的权值。
在图一中,利用CD算法进行预训练时,只需要迭代计算RBM1,RBM2和RBM3三个单元的W,a,b值,最后一个BP单元的W和b值,直接采用随机初始化的值即可。通常,我们把由RBM1,RBM2和RBM3构成的结构称为DBN结构(深度置信网络结构),最后再加上一层输出层(BP层)后,便构成了标准型的DNN结构:DBN-DNN。
2.有监督反向调参
进行有监督的调优训练时,需要先利用前向传播算法,从输入得到一定的输出值,然后再利用后向传播算法来更新网络的权重值和偏置值。
1.前向传播
1)利用CD算法预训练好的W,b来确定相应隐元的开启和关闭。
计算每个隐元的激励值如下:
其中,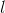
其中,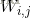
2)逐层向上传播,一层层地将隐藏层中每个隐元的激励值计算出来并用sigmoid函数完成标准化,如下所示:
当然,上述是以sigmoid函数作为激活函数的标准化过程为例。
3)最后计算出输出层的激励值和输出。
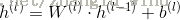
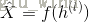
其中,输出层的激活函数为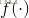
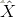
2.反向传播
1)采用最小均方误差准则的反向误差传播算法来更新整个网络的参数,则代价函数如下:
其中,E为DNN学习的平均平方误差,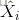
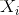
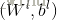
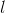
2)采用梯度下降法,来更新网络的权重和偏置参数,如下所示:
其中,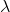
以上便是构建整个DBN-DNN结构的两大关键步骤:无监督预训练和有监督调优训练。选择好合适的隐层数、层神经单元数以及学习率,分别迭代一定的次数进行训练,就会得到我们最终想要的DNN映射模型。











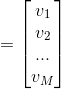
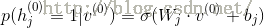
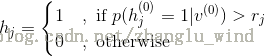
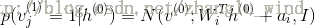
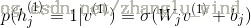
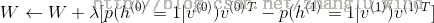
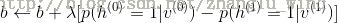
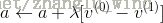
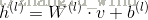


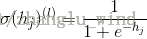
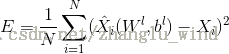
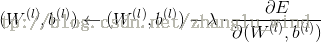
 支付宝扫一扫
支付宝扫一扫 微信扫一扫
微信扫一扫






