如果数据 x(i)∈Rn 是来自混合高斯分布,那么可用 EM 算法来拟合混合模型,但假设前提是有足够的数据,我们能发现数据中的多高斯结构,这就要训练数据集大小 m 远大于数据维度 n。
如果 n>>m 呢?那就很难对数据建模,即使是一个高斯。m 个数据点只能在低维度空间,如果要把数据建模为高斯分布,用极大似然估计来估计均值和协方差:
我们会发现 Σ 是奇异矩阵。例如当 m=2,n=5,如下例所示,最后 Σ =0。


import numpy as np x1=np.array([2,3,7,6,5]) x2=np.array([7,9,3,1,4]) x1.shape=(5,1) x2.shape=(5,1) mu=(x1+x2)/2.0 # ".0" is request var=(np.dot(x1-mu,np.transpose(x1-mu))+np.dot(x2-mu,np.transpose(x2-mu)))/2.0 print "The covariance of the matrix is %s." % np.linalg.det(var)
View Code
当 Σ 为奇异矩阵时,|∑| = 0,那么 Σ-1 就不存在,1/|Σ|1/2 = 1/0,但这些在计算多元高斯分布的密度时都是需要的。通常情况下,除非 m 比 n 大得超过一定范围,不然对均值和协方差的极大似然估计会非常差。当然,我们肯定希望对数据拟合一个合理的高斯模型,来获得数据中一些有趣的协方差结构信息。那怎么办呢?
下面我们先来看对 Σ 施加两个限制,可以使我们用少量的数据来拟合 Σ,但都不能给出满意的解决方案。接下来再讨论高斯的一些特性,后面会用到,特别是如何寻找高斯的边缘和条件分布。最后介绍因子分析模型,以及 EM 解法。
1、对 Σ 的限制
如果没有足够的数据来拟合一个完整的方差矩阵,可以对矩阵 Σ 的空间添加一些限制。例如,选择拟合一个对角矩阵 Σ,在这种情况下,协方差矩阵的极大似然估计,即对角矩阵 Σ 满足:
如何通过极大似然估计推出上式,有兴趣的读者可自行验证。
高斯密度的轮廓是椭圆,当协方差矩阵 Σ 是对角矩阵时,椭圆的主轴就与坐标轴平行。
有时我们会对协方差矩阵作进一步的限制,它不仅是对角的,而且对角线上的元素是等值的。这时,Σ=σ2I,其中 σ2 是控制参数。σ2 的极大似然估计为:
这个模型所关联的高斯密度的轮廓在二维情况下是圆,在高维情况下是球体,或超球体。
如何我们要对数据拟合一个完整的、无约束的协方差矩阵 Σ,那就需要 m>>n 以使得 Σ 的极大似然估计是非奇异的。如果满足上面两个限制中的任意一个,只要 m≥2 就能得到一个非奇异的 Σ。
但是,限制 Σ 为对角矩阵也意味着,建模数据的不同坐标 xi 和 xj 为不相关和独立的。有时就是要获得数据中的一些有趣的关联,如果使用了上面对 Σ 的限制,就没法发现这种关联。所以,下面我们介绍因子分析模型,比对角矩阵 Σ 使用更多的参数,但不需要拟合完整的协方差矩阵。
2、高斯边缘和条件分布
在介绍因子分析之前,先来讨论如何寻找联合多元高斯分布随机变量的条件和边缘分布。
假设有一个向量值型随机变量:
其中 x1 属于 r 维向量空间,x1∈Rr,x2∈Rs,x∈Rr+s,假设 x~N(μ,Σ),其中:
这里 μ1∈Rr,μ2∈Rs,Σ11∈Rr×r,Σ12∈Rr×s 等等。因为协方差矩阵是对称的,所以 Σ12=Σ21T。
在这种情况下,x1 和 x2 是联合多元高斯,那么 x1 的边缘分布是什么?不难看出 E[x1]=μ1,Cov(x1)=E[(x1-μ1)(x1-μ1)]=Σ,根据 x1 和 x2 的联合协方差的定义,有:
因为高斯的边缘分布本身就是高斯,所以得 x1 的边缘分布为 x1~N(μ1,Σ11)。
那么 x1 在给定 x2 下的条件分布呢?由多元高斯分布的定义,可得 x1|x2~N(μ1|2,Σ1|2),其中
下面介绍因子分析模型时,这些公式对于寻找高斯条件和边缘分布是很有用的。
3、因子分析模型
在因子分析模型中,我们假设 (x,z) 是如下的联合分布,其中 z∈Rk 是一个隐随机变量:
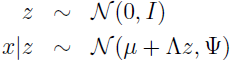 这里模型的参数是,向量 μ∈Rn,矩阵 Λ∈Rn×k,对角矩阵 Ψ∈Rn×n,k 值通常是小于 n 的。
这里模型的参数是,向量 μ∈Rn,矩阵 Λ∈Rn×k,对角矩阵 Ψ∈Rn×n,k 值通常是小于 n 的。
所以每个数据点 x(i) 是通过如下方式生成的:
a. 从 k 维多元高斯分布中采样得到 z(i);
b. 通过计算 μ+Λz(i) 将 z 映射到 n 维空间;
c. 给 μ+Λz(i) 增加协方差 Ψ 噪声,得到 x(i)。
同样的,我们也可以根据下列方式来定义因子分析模型。
其中 ε 和 z 是相互独立的。
现在来仔细看下这个模型定义了一个什么样的分布。随机变量 z 和 x 有一个联合高斯分布。
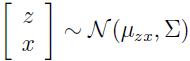
现在来寻找 μzx 和 Σ。
我们知道 E[z]=0,因为 z~N(0,I),同时有
放到一起可得:
 下一步,为了寻找 Σ,需要计算 Σzz=E[(z-E(z))(z-E(z))T],Σzx=E[(z-E(z))(x-E(x))T],Σxx=E[(x-E(x))(x-E(x))T]。
下一步,为了寻找 Σ,需要计算 Σzz=E[(z-E(z))(z-E(z))T],Σzx=E[(z-E(z))(x-E(x))T],Σxx=E[(x-E(x))(x-E(x))T]。
因为 z~N(0,I),易见 Σzz=Cov(z)=I,也可得 Σzx=
第一步是因为 E[z]=0,x=μ+Λz+ε,E[x]=μ。
第二步消去 μ。
第三步是因为 E[zzT]=Cov(z)=I,E[zεT]=E[z]E[εT]=0(因为 z 和 ε 是相互独立的,所以乘积的期望也是期望的乘积)。类似地可得 Σxx:
集中以上结果可得:
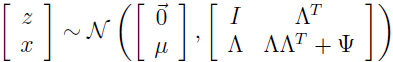
所以,可以看到 x 的边缘分布 x~N(μ,ΛΛT+Ψ)。所以,给定训练集 {x(i);i=1,2,…,m},我们能写下参数的 log 似然估计为:
为执行极大似然估计,我们将以这些参数来最大化该式,直接最大化该式很难,没有封闭形式下的算法可解出该式。所以,我们将使用 EM 算法。
4、EM 解因子分析
E-step 的推导很容易,需要计算 Qi(z(i))=p(z(i)|x(i);μ,Λ,Ψ)。结合上面得到的两个结果:
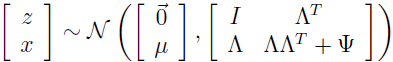
可得
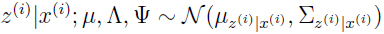
其中
用这些定义可得:
现在开始 M-step,这里需要最大化
以 μ,Λ 和 Ψ 为参数。我们这里只推导以 Λ 为参数的最优化,μ 和 Ψ 的更新推导留给读者。
上式可简化为:
下标 z(i)~Qi 表示期望是指服从 Qi 分布的 z(i)。下面将忽略这个下标,不会存在模糊的风险。去掉与参数 Λ 不相关的部分,需要最大化的是:
只有最后一项依赖于 Λ,求导,使用事实 tra=a(a∈R),trAB=trBA,▽AtrABATC=CAB+CTAB,有:
设为 0 并简化,得:
解出 Λ,得:
从 Q 是均值为 μz|x 协方差为 Σz|x 的高斯的定义可得:
最后一式是因为,对于随机变量 Y,Cov(Y)=E[YYT]-E[Y]E[Y]T,所以,E[YYT]=E[Y]E[Y]T+Cov(Y)。
代入该式到上面的 Λ,可得:
注意到上式右边有个 Σz|x ,这是后验概率 p(z(i)|x(i)) 的协方差。
我们也能找到 μ 和 Φ 的最优化参数。
注意到当参数改变时,μ 不是发生改变,不像 Λ 依赖于 Qi(z(i))=p(z(i)|x(i);μ,Λ,Φ),所以,它只需要开始计算一次,算法运行时不需要再更新。同样,对角 Ψ 为
设置 Ψii=Φii。对角矩阵 Ψ 只包含对角元素 Φ。
参考资料:
1、http://cs229.stanford.edu/notes/cs229-notes9.pdf
2、http://blog.csdn.net/stdcoutzyx/article/details/37559995
3、http://www.cnblogs.com/jerrylead/archive/2011/05/11/2043317.html




























 支付宝扫一扫
支付宝扫一扫 微信扫一扫
微信扫一扫





