11
矩阵的QR分解
一.Givens矩阵与Givens变换
定义:设实数c与s满足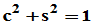 ,称
,称
(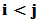 )
)
为Givens矩阵(初等旋转矩阵),也记作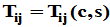 。由Givens矩阵所确定的线性变换称为Givens变换(初等旋转变换)。
。由Givens矩阵所确定的线性变换称为Givens变换(初等旋转变换)。
说明:(1)实数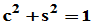 ,故存在
,故存在 ,使
,使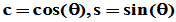 。
。
(2) 中
中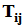 确定了将向量变成y的一种变换,正是Givens变换。二阶情况下,
确定了将向量变成y的一种变换,正是Givens变换。二阶情况下,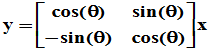 确定的正是平面直角坐标系中绕原点的一个旋转变换(旋转
确定的正是平面直角坐标系中绕原点的一个旋转变换(旋转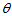 度)。
度)。
(3)以上实Givens也可推广称为复初等旋转矩阵。
显然,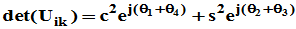
当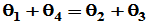 时,
时,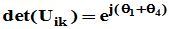
当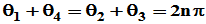 时,
时,
2. 性质
(1) ,
, 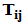 为正交矩阵。
为正交矩阵。
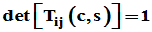
(2)设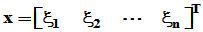 ,
,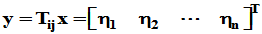 ,则有
,则有
当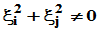 时,总可以选
时,总可以选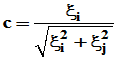 ,
,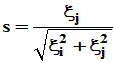 使
使
定理1. 设 ,则存在有限个Givens矩阵的乘积T,使得
,则存在有限个Givens矩阵的乘积T,使得
说明:(1)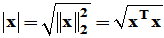 (x为实数时),
(x为实数时),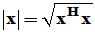 (x为复数时)。
(x为复数时)。
(2)
[证明]: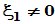 的情形
的情形
构造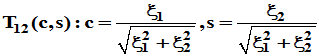
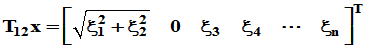
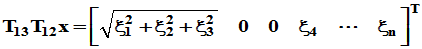
依此类推,构造
(k=2,3,…..n)
 直至可k=n。令
直至可k=n。令 ,则有
,则有

 的情形, 从第一个不为零的
的情形, 从第一个不为零的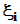 开始运用上述方法即可
开始运用上述方法即可
推论:对于任何非零列向量 及任何单位列向量
及任何单位列向量 ,均存在着有限个Givens矩阵的乘积T,使
,均存在着有限个Givens矩阵的乘积T,使 。
。
[证明]:由上述定理,对x存在有限个Givens矩阵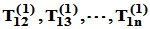 的乘积
的乘积
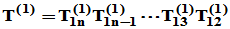 ,使
,使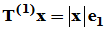
对z同理存在有限个Givens矩阵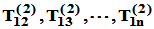 的乘积
的乘积
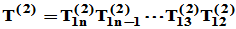 ,使
,使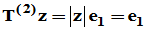
其中
二 Householder矩阵与Householder变换
平面直角坐标系中,将向量 关于
关于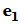 轴作为交换,则得到
轴作为交换,则得到
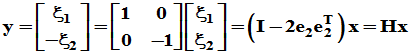
一般地,可将其推广
1. 定义:设单位列向量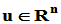 ,称
,称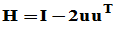 为Householder矩阵(初等反射矩阵),由Householder矩阵所确定的线性变换(
为Householder矩阵(初等反射矩阵),由Householder矩阵所确定的线性变换( )成为Householder变换
)成为Householder变换
2 . 性质
(1)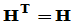 (实对称),
(实对称), (正交),
(正交), (对合),
(对合),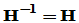 (自逆),
(自逆),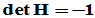
为证明第5条,可利用如下引理。
引理:设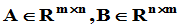 ,则
,则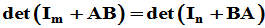
[证明]:参考如下的分块矩阵 的行列式,用A左乘第一行块加到第二行块,然后用(-B)左乘第二行块加到第一行块,有
的行列式,用A左乘第一行块加到第二行块,然后用(-B)左乘第二行块加到第一行块,有
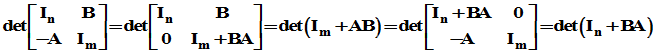 故,
故,
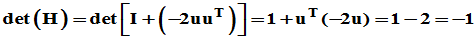
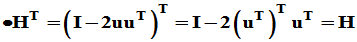

定理2. 对于任何非零列向量 及任何单位列向量
及任何单位列向量 ,存在Householder矩阵H,使得
,存在Householder矩阵H,使得 。
。
[证明] 当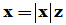 时,选u满足
时,选u满足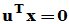 ,则
,则
当 时,选
时,选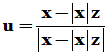 ,有
,有
定理3. 初等旋转矩阵(Givens矩阵)是两个初等反射矩阵的乘积。
证明参见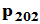 ,较容易。我们这里主要是给出一种几何解释。
,较容易。我们这里主要是给出一种几何解释。
从表明上看,似乎一种反射变换即可代替旋转变换。实际上是不对的,因为这样的反射变换对应的对称轴沿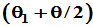 方向,与
方向,与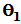 有关
有关
实际上,旋转变换可由这样两次反射变换的作用来代替。
首先,关于沿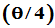 对称轴作反射变换,则原向量沿
对称轴作反射变换,则原向量沿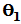 方向转至
方向转至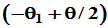 。
。
其次,关于沿 对称轴作反射变换,则向量反射至沿
对称轴作反射变换,则向量反射至沿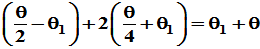 。正是原向量沿
。正是原向量沿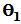 方向转
方向转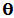 的结果。
的结果。
 旋转变换可用两个反射变换的连续作用来代替,即
旋转变换可用两个反射变换的连续作用来代替,即 。但是反射变换却不可能用多个旋转变换的连续作用来代替。这是因为
。但是反射变换却不可能用多个旋转变换的连续作用来代替。这是因为 。由两个-1的乘积可得1,但多个1的乘积只能是1,不是-1。
。由两个-1的乘积可得1,但多个1的乘积只能是1,不是-1。
三、 QR分解
1. 定义:如果实(复)矩阵A可化为正交(酉)矩阵Q与实(复)上三角矩阵R的乘积,即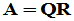 ,则称上式为A的QR分解。
,则称上式为A的QR分解。
2. 定理4:设A是n阶的非奇异矩阵,则存在正交(酉)矩阵Q与实(复)上三角矩阵R使得 ,且除去相差一个对角元素的绝对值(模)全为1的对角因子外,上述分解唯一。
,且除去相差一个对角元素的绝对值(模)全为1的对角因子外,上述分解唯一。
[证明]:设A记为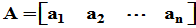 ,A非奇异
,A非奇异 线性无关
线性无关
采用Gram-schmidt正交化方法将它们正交化,可得
R是实(复)上三角矩阵
唯一性: 采用反证法。设存在两个QR分解,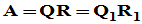 ,则
,则
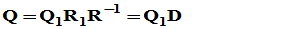
 D为上三角矩阵
D为上三角矩阵
而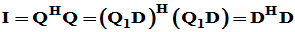
 D为酉(正交)矩阵
D为酉(正交)矩阵
故,D只能为对角阵
这一证明方法可推广为:
定理5. 设A是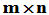 的实(复)矩阵,且其n个列线性无关,则A具有分解
的实(复)矩阵,且其n个列线性无关,则A具有分解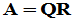 。其中Q是
。其中Q是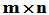 阶实(复)矩阵,且满足
阶实(复)矩阵,且满足 ,R是n阶实(复)非奇异三角矩阵。除了相差一个对角元素的绝对值(模)全为1的对角阵因子外,上述分解唯一。
,R是n阶实(复)非奇异三角矩阵。除了相差一个对角元素的绝对值(模)全为1的对角阵因子外,上述分解唯一。
3. 求QR分解的方法
[方法一]采用Givens方法
将n阶非奇异矩阵A写为

令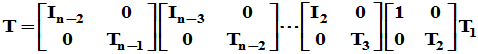 ,则有
,则有
其中,R为上三角矩阵,Q= 正交矩阵
正交矩阵
[方法二]采用Householde方法
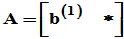 存在
存在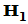 ,使得
,使得

 存在
存在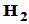 ,使得
,使得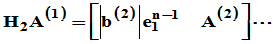
 存在
存在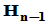 ,使得
,使得
令
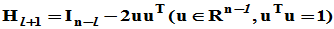
则

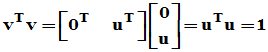
两种方法前一种方法可推广到复矩阵的情况。
3. Gram-schmidt正交归一化方法
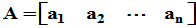 ,各列向量线性无关可进行正交化
,各列向量线性无关可进行正交化
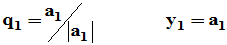


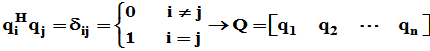 ,满足
,满足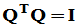
改写:
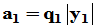
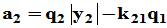
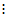
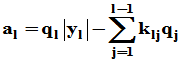
作业:p219-220,1、7、8
欢迎访问我的专业知识博客!
博主:白途思(begtostudy)
微信/QQ:370566617
Email:begtostudy#gmail.com
欢迎访问我的其他博客:我的编程知识博客 我的学术知识博客



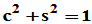 的实数,
的实数, 为实角度。
为实角度。

 再考虑
再考虑














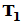 ,使得
,使得
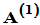

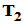 ,使得
,使得
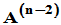 写成
写成
 ,使得
,使得




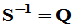 为正交矩阵
为正交矩阵


