最优超平面(分类面)

　　如图所示, 方形点和圆形点代表两类样本, H 为分类线,H1, H2分别为过各类中离分类线最近的样本且平行于分类线的直线, H1、H2上的点（xi, yi）称为支持向量， 它们之间的距离叫做分类间隔(margin)。中间那条分界线并不是唯一的，我们可以把它稍微旋转一下，只要不分错。所谓最优分类面(Optimal Hyper Plane)就是要求分类面不但能将两类正确分开(训练错误率为0),而且使分类间隔最大。推广到高维空间，最优分类线就变为最优分类面。支持向量是那些最靠近决策面的数据点，这样的数据点是最难分类的，因此,它们和决策面的最优位置直接相关。

　　我们有两个 margin 可以选，不过 functional margin 明显是不太适合用来最大化的一个量，因为在 hyper plane 固定以后，我们可以等比例地缩放 w 的长度和 b 的值，这样可以使得 f(x)=w^Tx+b 的值任意大，亦即 functional margin γ_f可以在 hyper plane 保持不变的情况下被取得任意大，而 geometrical margin γ_g则没有这个问题，因为除上了 ∥w∥ 这个分母，所以缩放 w 和b 的时候γ_g的值是不会改变的，它只随着 hyper plane 的变动而变动，因此，这是更加合适的一个 margin 。对一个数据点进行分类，当它的 margin 越大的时候，分类的 置信度(confidence) 越大。对于一个包含 n 个点的数据集，我们可以很自然地定义它的 margin 为所有这 n 个点的 margin 值中最小的那个γ_g=minγ_g，i，于是，为了使得分类的 confidence 高，我们希望所选择的 hyper plane 能够最大化这个 margin 值。简要地说，就是找到这样一个最优分类面，使离最优分类面最近的点的几何距离最大。即最优分类面的目标函数为：

   max γ_g  ,  s.t.  y_i(w^T ·x_i+b) = γ_g，i  >=  γ_g，i=1,…,n                                                                    （4）

其中γ_g= 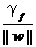 ，由于我们的目标就是要确定超平面，求max γ_{g ，}因此可以把无关的变量固定下来，固定的方式有两种：一种是固定 ∥w∥,另一种是固定 γ_f. 处于方便推导和优化的目的，我们选择第二种，令γ_f=1 ，则我们的目标函数化为：

    max,    s.t. , yi(w^Txi+b)≥1, i=1,…,n                   （5）

H₁和H₂到最优分类面H的距离相等，都等于γ_g.

　　　　　　　　　　图3

最优超平面的详细推导

　　考虑训练样本{x_i, y_i}^N_i=1, 其中x_i 是输入模式的第i 个样本，y_i∈{-1,+1}。设用于分离的超平面方程是g(x)=w^T·x + b =0; 其中w 是超平面的法向量,b 是超平面的常数项. 现在的目的就是寻找最优的分类超平面,即寻找最优的w 和b。求这样的g(x)的过程就是求w（一个n维向量）和b（一个实数）两个参数的过程（但实际上只需要求w，求得以后找某些样本点代入就可以求得b）。因此在求g(x)的时候，w才是变量。设最优的w 和b 为w₀ 和b₀，则最优的分类超平面为: w₀ ^T·x + b₀ =0；若得到上面的最优分类超平面,就可以用其来对测试集进行预测了。设测试集合为{t_i} ^N_i=1,则用最优分类超平面预测出的测试集的标签为:

        t_i_label = sgn(w₀ · t_i + b₀).

SVM 的主要思想是建立一个超平面作为决策曲面, 使得两类之间的隔离边缘被最大化。求最优分类超平面等价于求最大几何间隔，由上式可知也等价于||w||的最小值。

设固定函数间隔为1，则支持向量为

　　　　H₂: w^T·x_i + b = -1, y_i = -1 或者H₁: w^T·x_i +b = +1, y_i = +1

设图3上H₁、H₂上各有一点，分别为x₁,x₂； 则w^T·x₁ + b=1 , w^T·x₂ + b=-1

　　　　　　　　　　　　　　　　　　　　 => w^T·(x₁– x₂)=2 => 两类几何间隔( x₁– x₂) = ；

max     <=>   min ||w||  <=>  min  1/2 * ||w||² ；                                                                            （6）

对于任意的(x_i, y_i), 有 w^T·x_i+b<=-1, y_i=-1或者w^T·x_i+b>=1, y_i=1，即y_i (w^T·x_i +b)>=1。

故寻找最优超平面即正反两类间隔最大化问题, 最终归结为一个带约束的二次凸优化问题(这种问题可以用任何现成的 QP (Quadratic Programming) 的优化包进行求解。)：

    min 1/2 * ||w||²， s.t. ,  y_i (w^T·x_i +b)>=1，(i=1,2…n，n为样本数)                                                             (7)

虽然这个问题确实是一个标准的 QP 问题，但是它也有它的特殊结构，通过 拉格朗日对偶（Lagrange Duality） 变换到对偶变量 (dual variable) 的优化问题之后，可以找到一种更加有效的方法来进行求解——这也是 SVM 盛行的一大原因，通常情况下这种方法比直接使用通用的 QP 优化包进行优化要高效得多。

使用Lagrange 乘子法可解决二次规划问题：

1）首先建立Lagrange 函数:

　　L(w,b,α)=||w||²-∑α_i[y_i (w^T·x_i +b)-1] i=1,2…n           　　　　　　　　　　　　　　　　　　　　　　　　　　  (8)

　　令θ_p(w)=mαx L(w,b,α)  s.t. α_i>=0 ,  原问题即求min θ_p(w)=min max L(w,b,α)=p^*； s.t. α_i≥0

　　对偶问题(交换min,max顺序): θ_D(w) = max α_i≥0 min L(w,b,α)=d^*；

      显然d^* <= p^*，可以理解为最大值中最小的一个总比最小值中最大的一个要大。

2）L对w 和b分别求偏导并置零,求得w=∑α_i·y_i·x_i, ∑α_iy_i =0;

3）再整理L 最终可以得到关于原问题的对偶变量α的优化问题:

     max L(w,b,α)=∑α_i– 1/2 * ∑^N_i=1∑^N_j=1 α_iα_jy_iy_jx_i^Tx_j ,     s.t.,  ∑α_iy_i =0; α_i>=0

　  此时的拉格朗日函数只包含了变量。然而我们求出了才能得到w和b。

4) 求解出求偶问题的最优解(该问题用SMO算法来求解), 设用α^·i 表示最优的Lagrange 乘子,则此时原问题的最优解为:

　　   w₀ = 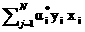，b₀=y_j–, 任意 j;

 　　 g(x)=<w₀，x>+b=<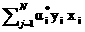，x>+b = ∑^N_j=1 α_iy_i<x_i,x>+b           　　　　　　　　　　　　　　　　   （9）

　　则判决函数为：f(x) = sgn(∑w₀x+b₀), 其中x 为测试集中的样本.

　　也就是说，以前新来的要分类的样本首先根据w和b做一次线性运算，然后看求的结果是大于0还是小于0,来判断正例还是负例。现在有了，我们不需要求出w，只需将新来的样本和训练数据中的所有样本做内积和即可。这一点至关重要，是之后使用 Kernel 进行非线性推广的基本前提。那么与前面所有的样本都做运算是不是太耗时了？答案是不会，由（8）式可知，对于支撑向量函数间隔等于1，对于非支持向量，函数间隔γ_f，而α_i非负，为了满足最大化，α_i 必须等于 0 。可见，内积运算仅与支持向量有关，可大大降低运算复杂度。

超平面在二维空间里就是直线，方程是a*x+b*y+c=0
超平面在三维空间里就是平面，方程是a*x+b*y+c*z+d=0
在n维空间里推广就是就是a*x+b*y+c*z+……..+k=0
这里的(a,b,c…)就是向量w,是由平面确定的数，（x,y,z..)是平面上任一点的坐标，就是你方程里的x，也是一个向量。

原文：https://www.cnblogs.com/Seiyagoo/archive/2013/06/08/3125497.html

https://blog.csdn.net/lyhbkz/article/details/82321845