度量学习方法总结
目录
一.距离度量
闵可夫斯基距离
欧式距离（Euclidean Distance）：
标准化欧氏距离 (Standardized Euclidean distance )
曼哈顿距离(ManhattanDistance)
切比雪夫距离（Chebyshevdistance）
马氏距离
马氏距离代码示例：
夹角余弦
相关系数 ( Correlation coefficient )与相关距离(Correlation distance)
交叉熵与相对熵（kl散度）
汉明距离
度量学习 (Metric Learning) == 距离度量学习 (Distance Metric Learning，DML) == 相似度学习
根据不同的任务来自主学习出针对某个特定任务的度量距离函数。通过计算两张图片之间的相似度，使得输入图片被归入到相似度大的图片类别中去。
一.距离度量
闵可夫斯基距离
假设数值点 P 和 Q 坐标如下：
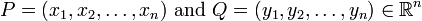
那么，闵可夫斯基距离定义为：
欧式距离（Euclidean Distance）：
两点之间的直线距离。p 是 2的闵可夫斯基距离。
(1)二维平面上两点a(x1,y1)，b(x2,y2)之间的欧式距离公式：
(2) n维空间上两点a(x1,x2……..xn)，b(y1,y2……..yn)的欧式距离公式：
标准化欧氏距离 (Standardized Euclidean distance )
样本集的标准化过程(standardization)用公式描述就是：
标准化后的值 = ( 标准化前的值 － 分量的均值 ) /分量的标准差
经过简单的推导就可以得到两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的标准化欧氏距离的公式：
如果将方差的倒数看成是一个权重，这个公式可以看成是一种加权欧氏距离(Weighted Euclidean distance)。
曼哈顿距离(ManhattanDistance)
p 是 1 的闵可夫斯基距离。
(1)二维平面上两点a(x1,y1)，b(x2,y2)之间的曼哈顿距离公式：
(2) n维空间上两点a(x1,x2……..xn)，b(y1,y2……..yn)的曼哈顿距离公式：
闵可夫斯基距离与数据的分布无关，具有一定的局限性，如果 x 方向的幅值远远大于 y 方向的值，这个距离公式就会过度放大 x 维度的作用。所以，在计算距离之前，我们可能还需要对数据进行 z-transform 处理，即减去均值，除以标准差：
Z变换(Z-transform) 将离散系统的时域数学模型——差分方程转化为较简单的频域数学模型——代数方程，以简化求解过程的一种数学工具。
https://zhuanlan.zhihu.com/p/45114376
切比雪夫距离（Chebyshevdistance）
各对应坐标数值差的最大值。p 趋近于无穷大时的闵可夫斯基距离。
(1)二维平面上两点a(x1,y1)，b(x2,y2)之间的切比雪夫距离公式：
(2) n维空间上两点a(x1,x2……..xn)，b(y1,y2……..yn)的切比雪夫距离公式：
如果维度相互之间数据相关（例如：身高较高的信息很有可能会带来体重较重的信息，因为两者是有关联的），这时候就要用到马氏距离（Mahalanobis distance）了。
马氏距离
马氏距离是基于样本分布的一种距离。有M个样本向量X1~Xm，协方差矩阵记为S，均值记为向量μ，则其中样本向量X到u的马氏距离表示为：
假设样本点（列向量）之间的协方差对称矩阵是
而其中向量Xi与Xj之间的马氏距离定义为：
若协方差矩阵是单位矩阵（各个样本向量之间独立同分布）,则公式就成了：
也就是欧氏距离了。
若协方差矩阵是对角矩阵（协方差矩阵的对角线上即为方差），公式变成了标准化欧氏距离。
马氏距离的计算是建立在总体样本的基础上的，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离计算即可。
马氏距离代码示例：
# -*- coding=utf-8 -*-
# code related at: http://www.cnblogs.com/daniel-D/
import numpy as np
import pylab as pl
import scipy.spatial.distance as dist
def plotSamples(x, y, z=None):
stars = np.matrix([[3., -2., 0.], [3., 2., 0.]])
if z is not None:
x, y = z * np.matrix([x, y])
stars = z * stars
pl.scatter(x, y, s=10) # 画 gaussian 随机点
pl.scatter(np.array(stars[0]), np.array(stars[1]), s=200, marker='*', color='r') # 画三个指定点
pl.axhline(linewidth=2, color='g') # 画 x 轴
pl.axvline(linewidth=2, color='g') # 画 y 轴
pl.axis('equal')
pl.axis([-5, 5, -5, 5])
pl.show()
# 产生高斯分布的随机点
mean = [0, 0] # 平均值
cov = [[2, 1], [1, 2]] # 协方差
x, y = np.random.multivariate_normal(mean, cov, 1000).T
plotSamples(x, y)
covMat = np.matrix(np.cov(x, y)) # 求 x 与 y 的协方差矩阵
Z = np.linalg.cholesky(covMat).I # 仿射矩阵
plotSamples(x, y, Z)
# 求马氏距离
print '\n到原点的马氏距离分别是：'
print dist.mahalanobis([0,0], [3,3], covMat.I), dist.mahalanobis([0,0], [-2,2], covMat.I)
# 求变换后的欧几里得距离
dots = (Z * np.matrix([[3, -2, 0], [3, 2, 0]])).T
print '\n变换后到原点的欧几里得距离分别是：'
print dist.minkowski([0, 0], np.array(dots[0]), 2), dist.minkowski([0, 0], np.array(dots[1]), 2)夹角余弦
机器学习中可以把两点看成是空间中的两个向量，通过衡量两向量之间的相似性来衡量样本之间的相似性。
(1)二维平面上两向量a(x1,y1)，b(x2,y2)之间的夹角余弦公式：
也可直接通过向量运算：
(2) n维空间上两点a(x1,x2……..xn)，b(y1,y2……..yn)的夹角余弦公式：
余弦相似度（Cosine similarity）：
余弦相似度与向量的幅值无关，只与向量的方向相关，夹角余弦越大表示两个向量的夹角越小，夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1，当两个向量的方向完全相反夹角余弦取最小值-1。
相关系数 ( Correlation coefficient )与相关距离(Correlation distance)
(1) 相关系数的定义
相关系数是衡量随机变量X与Y相关程度的一种方法，相关系数的取值范围是[-1,1]。相关系数的绝对值越大，则表明X与Y相关度越高。当X与Y线性相关时，相关系数取值为1（正线性相关）或-1（负线性相关）。
(2)相关距离的定义
交叉熵与相对熵（kl散度）
参考之前的博客 https://blog.csdn.net/qq_28266311/article/details/83994605
汉明距离
两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。
例如：
1011101与 1001001 之间的汉明距离是2
2143896与 2233796 之间的汉明距离是3
irie与 rise之间的汉明距离是 3
杰卡德距离(Jaccard Distance)
杰卡德相似系数(Jaccard similarity coefficient)：两个集合A和B的交集元素在A，B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示：
- 杰卡德距离(Jaccard Distance)：与杰卡德相似系数相反，用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度：
参考
https://blog.csdn.net/wangpei1949/article/details/52926651
https://www.cnblogs.com/daniel-D/p/3244718.html
https://www.cnblogs.com/heaad/archive/2011/03/08/1977733.html
支付宝扫一扫
微信扫一扫
