二叉树的性质

(二叉树的每个节点最多只有 2 个子树（不存在度 >2 的节点）有左右之分，不可以颠倒)
(二叉树的第 i 层最多有 2^{i-1}个结点)
(设二叉树的深度为 k 则: 二叉树最多有 2^{k}-1 个结点)
(对任何一棵二叉树 T ,设其叶节点数为 n_{0} 其度为 2 的结点个数为 n_{2} 则：n_{0} = n{2} + 1)

某些特殊的二叉树

满二叉树：

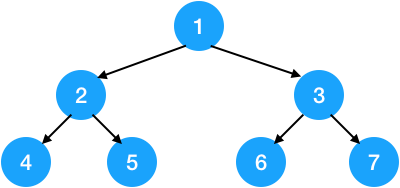
满二叉树示意图

$深度为 k 且有 2^{k}-1 个结点,就是一棵满二叉树，满二叉树的每一层都是满的$

完全二叉树：

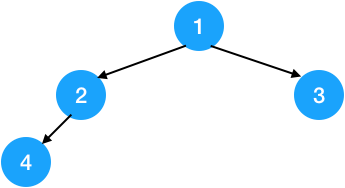
完全二叉树示意图

$除最后一层外，其他层都是满的，或在右边连续缺少若干结点，就是一棵完全二叉树，设有 n 个结点的完全二叉树的深度为log_{2}(n+1)$
$深度为 k 的完全二叉树，至少 2^{k-1} 个结点，最多 2^{k}-1 个结点$

二叉搜索树：

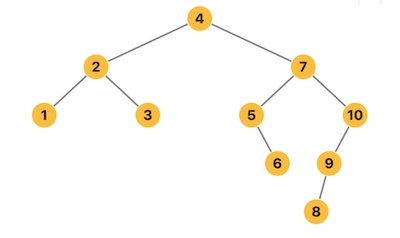
二叉搜索树示意图

排序二叉树有如下性质
– $若左子树不空，则左子树上所有节点均小于根节点的值$
– $若右子树不空，则右子树上所有节点均大于根节点的值$
– $左右子树也都是二叉搜索树$
– $二叉搜索树可以为空树$

遍历二叉树

- 先序遍历
  $先序遍历是指先访问根节点，再依次访问左子树和右子树$

- 中序遍历
  $中序遍历是指先访问左子树，再依次访问根节点和右子树$

- 后序遍历
  $先序遍历是指先访问左子树和右子树，最后再访问根节点$

- 层次遍历
  $跟“扩展式广度优先搜索（俗称“广搜”）相同”$

- 四种遍历参考代码：

int son[N][2], root;
vector<int> v1, v2, v3, v4;
//先序遍历
void preorder(int u) {
    if (u == 0) return;
    v1.push_back(u);
    preorder(son[u][0]);
    preorder(son[u][1]);
}
//中序遍历
void inorder(int u) {
    if (u == 0) return;
    inorder(son[u][0]);
    v2.push_back(u);
    inorder(son[u][1]);
}
//后序遍历
void postorder(int u) {
    if (u == 0) return;
    postorder(son[u][0]);
    postorder(son[u][1]);
    v3.push_back(u);
}
//层次遍历
void levelorder() {
    queue<int> q;
    if (root != 0) q.push(root);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        v4.push_back(u);
        if (son[u][0] != 0) q.push(son[u][0]);
        if (son[u][1] != 0) q.push(son[u][1]);
    }
}
      ```
## 根据遍历结果复原二叉树：

注意！先序遍历和后序遍历不能确定唯一的二叉树！

对于先序遍历和中序遍历，我们只需在先序遍历中确定根节点，并且靠中序遍历找出其位置，再依次还原左子树和右子树，即可确定二叉树。
对于后序遍历和中序遍历，也可按照同样的方法进行还原，确定唯一的二叉树。

参考代码：

```cpp
// a数组为中序遍历，b数组为先序遍历
// x1、y1为当前子树在a数组中下标的范围，x2为前子树在b数组中下标的起点
int a[N], b[N], son[N][2];
void dfs(int x1, int y1, int x2) {
    int pos = x1;
    while (a[pos] != b[x2]) { // 在中序遍历里找到当前子树的根
        pos++;
    }
    int len1 = pos - x1, len2 = y1 - pos; // 在中序遍历里确定当前子树的左子树和右子树大小
    if (len1 > 0) { // 如果有左子树，那么根据先序遍历确定这个节点的左孩子
        son[b[x2]][0] = b[x2 + 1];
        dfs(x1, pos - 1, x2 + 1); // 递归进入左子树
    }
    if (len2 > 0) { // 如果有右子树，那么根据先序遍历确定这个节点的右孩子
        son[b[x2]][1] = b[x2 + 1 + len1];
        dfs(pos + 1, y1, x2 + 1 + len1); // 递归进入右子树
    }
}